Math IS Fun: Menghadapi Nilai-Nilai Besar

Berapa angka terbesar yang pernah kalian bayangkan? Satu milyar? Satu trilyun? Seribu trilyun? Sejuta trilyun? Oh stop! Alasan mengapa orang keuangan pusing adalah, karena terlalu sibuk menghitung banyak angka, sedangkan uangnya tidak pernah mereka dapatkan hehe…

Tapi, tapi… terbayangkan kah kalian dengan angka 99⁹⁹ atau 10²⁰⁰³? Plis deh, perpangkatan tiga aja masih hitung manual dan nggak ketemu-ketemu. Ini malah perpangkatan yang bisa ngerusak kalkulator.Tapi benar, soal-soal olimpiade adik-adik kita memang memiliki bilangan sedemikian besarnya. Saya ingat sewaktu SMP, ada soal seperti ini:

Mana bilangan yang paling besar? 2⁵⁵⁵⁵, 3³³³³, 5²²²²?

Ekspresi saya ketika melihat soal tersebut:

Seriously what is this?

Tetapi sebenarnya menghadapi angka-angka besar tersebut sangatlah menyenangkan. Maka dari itu, yang ingin saya jelaskan selain kemampuan berhitung adalah kemampuan menganalisa dan mungkin dapat saya katakan sebagai kemampuan menggunakan cara lain atau strategi.

• Membandingkan dua perpangkatan besar

Seperti, mana yang lebih besar? 2³⁵⁰ atau 5¹⁵⁰?

Plis, jangan dihitung satu-satu. Pokoknya jangan…

Sebenarnya, 2³⁵⁰ adalah (2⁷)⁵⁰. Dan 5¹⁵⁰ adalah (5³)⁵⁰. Lho, kok bisa dipecah jadi begitu?

Ingat apa yang telah kalian pelajari:

a^{m x n} = (a^m)ⁿ

Karena 2⁷ adalah 128 dan 5³ adalah 125, dan 128 lebih besar dari 125 maka sudah pasti jawabannya adalah 2³⁵⁰ lebih besar dari 5¹⁵⁰.

Nah, dengan cara yang sama kalian akan mengetahui mana yang paling besar dari 2⁵⁵⁵⁵, 3³³³³, 5²²²². Bahkan bisa kalian urutkan. 🙂

• Penjumlahan deret besar

Sekarang berapa jumlah dari:

1² – 2² + 3² – 4² + 5² – 6² + …. + 2009² – 2010² + 2011²

Apa? Saya harus tahu jumlah dari rentetan bilangan mengerikan di atas? Ekspresi saya:

Jangan panik, tidak ada gempa bumi atau kebakaran di sini. Coba buat strategi di atas tempat duduk kalian yang manis dan menyenangkan mengenai angka-angka tersebut menjadi:

(1² – 2²) + (3² – 4²) + (5² – 6²) + …. + (2009² – 2010²) + 2011²

Kaciaan deh angka dua rebu sebelas kagak ada pasangannya bhahahah. Di dalam dunia MTK juga ada istilah ‘jomblo’ ya… Sebuah kabar baik untuk para jombloers seperti saya ini. Hehe… _{jadi pengen nangis…}

Ingat bahwa:
a² – b² = (a + b)(a – b)

Jadi,
(1² – 2²) = (1 + 2)(1 – 2)
Sehingga,
(1² – 2²) = -1 – 2
Cukup, jangan lanjutkan jadi -3. Justru kita tahan di -1-2 agar memudahkan ke tahap berikutnya.

Berarti,
(3² – 4²) = -3 – 4
Dsb… (dan saya bingung)

Sehingga ditemukanlah pola baru:

-1 -2 -3 -4 -5 -6, … -2009 -2010 + 2011²
Kasihan ya, 2011 masih belum diapa-apain…
Berarti:
– (1 + 2 + 3 + 4 + 5 + 6 + … + 2009 + 2010) + 2011²

Nah, salah satu sifat baris dan deret, yang Sn itu loh.
– ½ x 2010 x 2011 + 2011²

Tambah sedikit magic:
-1005 x 2011 + 2011 x 2011 (kuadratnya saya jabarkan saja)
Ya sudah, karena pengalinya sama-sama 2011, maka bisa jadi begini:
2011 x (-1005 x 2011)
= 2011 x 1006
(hitung manual aja ya, angkanya udah gampang)
= 2023066

•  Sisa hasil bagi yang gede!

Berapakah satuan dari 3²⁰¹⁷? Oh, please, jangan soal kayak gini lagi…

Oh, dia cuma minta satuannya aja ya? Ok, cukup lihat polanya saja.

3 pangkat 1 = 3
3 pangkat 2 = 9
3 pangkat 3 = 27 (satuannya 7)
3 pangkat 4 = 81 (satuannya 1)
3 pangkat 5 = 243 (satuannya 3)
3 pangkat 6 = 729 (satuannya 9)

Eh, kok keulang lagi polanya? 3, 9, 7, 1, 3, 9, 7, 1? Oh ya udah gampang. Berarti polanya reset (ciye, bahasanya reset) setiap pola ke empat. Jadi kita lihat pangkatnya (3²⁰¹⁷) kalau dibagi empat dapat sisa berapa, kemudian di-match deh ~

2017 / 4 adalah… eh masih inget karakter bilangan habis dibagi 4 nggak? Waktu SD saya ingat kalau 2 digit terakhir habis dibagi 4, pasti habis dibagi 4. Pasti ya, karena matematika ini adalah ilmu pasti, bukan ilmu mungkin.

2 digit angka yang habis dibagi 4 adalah 04, 08, 12, 16, 20, 24, dst… sedangkan 2 digit terakhir dari 2017 adalah 17 atau 16 kelebihan 1 ya? Ya sudah kesimpulannya adalah bahwa 2017 jika dibagi 4 adalah sisa 1.

Berdasarkan tabel di atas, sisa satu memiliki satuan 3. Jadi angka terakhir atau satuan dari 3²⁰¹⁷ adalah 3. Ih, gampang! 😀

Oh, untuk masalah sisa hasil bagi atau modulo, saya pernah buat artikelnya di sini…

• Pola berulang yang bikin ucing

Ucing disini artinya Pucing, bukan Kucing. Ehm.

Ini saya ambil dari sebuah buku paket MTK SMA, tapi jangan khawatir, saya paham konsepnya kok. Sekarang, berapa nilai dari:

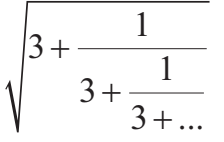
Ada kantong plastik? Lebih parah dari mabok di bus keknya. UOOEEEEKKK!!!

Tenang, tenang, tidak seburuk itu. Percaya deh sama saya. 🙂 (Ogah! Percaya sama situ nanti rukun iman saya tambah satu lagi ntar!)

Polanya sudah jelas,

Kok variabelnya dinamain P sih? Ya buku itu maunya pakek P, jika kalian mau pakai inisial pacar kalian juga boleh banget kok. Tapi apa sudah selesai? Belum. Kita mau tahu berapa nilai P, tanpa harus ada P lagi setelah simbol sama dengan. Ya kaliin aja semuanya dengan P lagi sampai dapat:

Kemudian pakai rumus kuadrat sempurna yaitu ax² + bx + c:

  Selesai deh. Tidak buruk ternyata.

Sekian tips dari saya, jangan kaget, jangan panik. Karena memang hal tersebut memang sederhana, hanya angkanya saja yang besar. Matematika itu menyenangkan, hanya saja… (isi sendiri)